【TRIO-Basic从入门到精通教程九】卡尔曼滤波器算法编程与测试
亲爱的朋友们,好久没有见面了!今天给大家带来实质性的算法,卡尔曼滤波器!很多朋友肯定又要问,卡尔曼到底是什么东东,具体有什么用处?这就是今天实验的目标!
解释原理,我们摘抄一段百科里面的描述:
//=====================================================================================================================================
卡尔曼滤波(Kalman filtering)一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过程。
斯坦利·施密特(Stanley Schmidt)首次实现了卡尔曼滤波器。
卡尔曼在NASA
埃姆斯研究中心访问时,发现他的方法对于解决
阿波罗计划的轨道预测很有用,后来
阿波罗飞船的导航电脑使用了这种滤波器。 关于这种滤波器的论文由Swerling (1958), Kalman (1960)与 Kalman and Bucy (1961)发表。
数据滤波是去除
噪声还原真实数据的一种
数据处理技术, Kalman滤波在测量方差已知的情况下能够从一系列存在测量噪声的数据中,估计动态系统的状态. 由于, 它便于计算机
编程实现, 并能够对现场采集的数据进行实时的更新和处理, Kalman滤波是目前应用最为广泛的滤波方法, 在通信, 导航, 制导与控制等多领域得到了较好的应用
.
//===================================================================================================================================
用通俗的话语讲:通入的原始数据抖动大,难于直接使用。相信很多朋友都是用过采用平均值的方法去除抖动,让输入数据平稳,但平均值会把误差噪声也引入,影响结果并且严重滞后输入反应。
是不是很神奇,我们接下来进入重点:
//===================================================================================================================================
DIM srcdata,resrcdata,outdata AS FLOAT '==================================================================== DIM measurenoise_r,processniose_q AS FLOAT measurenoise_r=10 processniose_q=0.5 DIM calall_data,calindex AS INTEGER DIM state_x,state_k,state_noise AS FLOAT calall_data=200 calindex=0 DIM serdata_tadr,noisedata_tadr,fliterdata_tadr,tablebuf_tadr AS INTEGER serdata_tadr=0 noisedata_tadr=1000 fliterdata_tadr=2000 tablebuf_tadr=3000 TABLE(serdata_tadr,0) TABLE(noisedata_tadr,0) TABLE(fliterdata_tadr,0) FOR calindex=1 TO calall_data srcdata=100*SIN(PI*calindex/200) TABLE(serdata_tadr+calindex,srcdata) resrcdata=srcdata+(RND(100)-50)*0.05 TABLE(noisedata_tadr+calindex,resrcdata) WA(2) '=================================================== 'FUNCTION kalmanfilter(serdata AS FLOAT,man_r AS FLOAT,proc_q AS FLOAT,tableadr AS INTEGER) AS FLOAT outdata=kalmanfilter(resrcdata,measurenoise_r,processniose_q,tablebuf_tadr) '=================================================== TABLE(fliterdata_tadr+calindex,outdata) NEXT calindex
//===================================================================================================================================
首先我们画了一个正玄曲线
srcdata=100*SIN(PI*calindex/200)
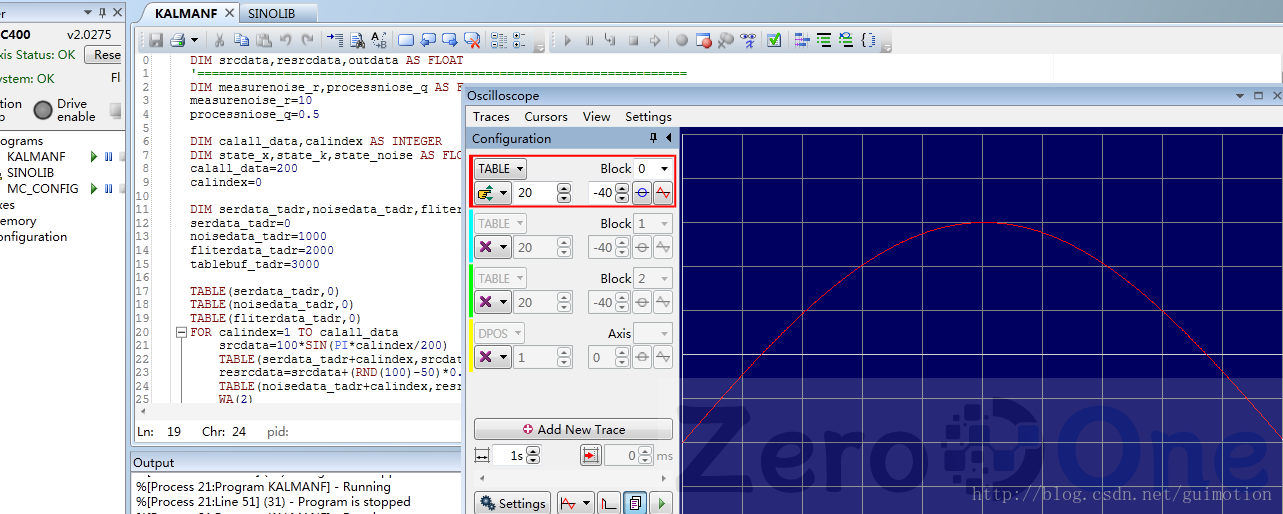
为了试验数据,我们给正玄曲线添加随机噪声
resrcdata=srcdata+(RND(100)-50)*0.05

蓝色的曲线将是我们将要输入滤波器进行滤波的数据
outdata=kalmanfilter(resrcdata,measurenoise_r,processniose_q,tablebuf_tadr)
我们来试试滤波器后的效果
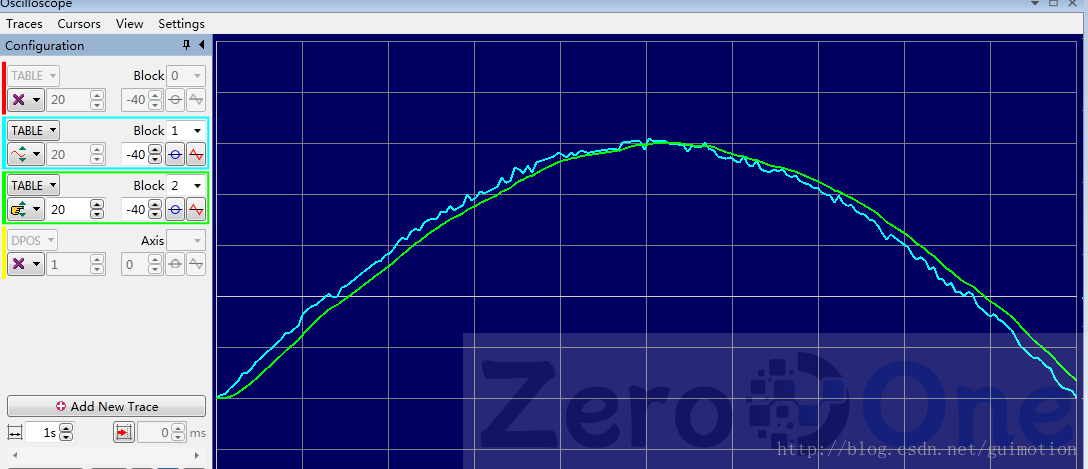
从示波器中可以看出,绿色曲线消除了蓝线中的抖动,并又很好的保留了趋势。
看了上面测试这么多,一点很期待算法原始程序吧
不要着急,马上上图:
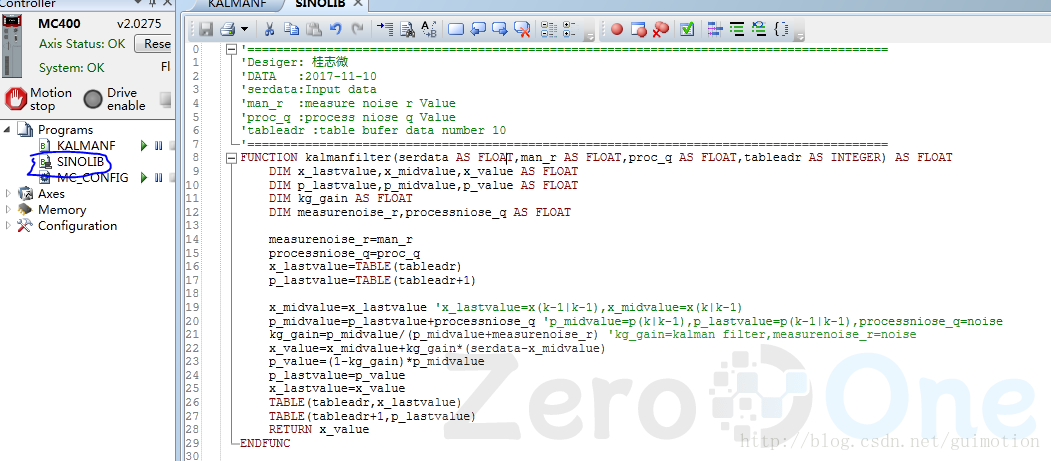
算法到此为止,细心的朋友一定发现R Q两个参数,这个两个参数对滤波器性能很关键,根据实际需求控制滤波效果大小
1、R小 Q小的效果
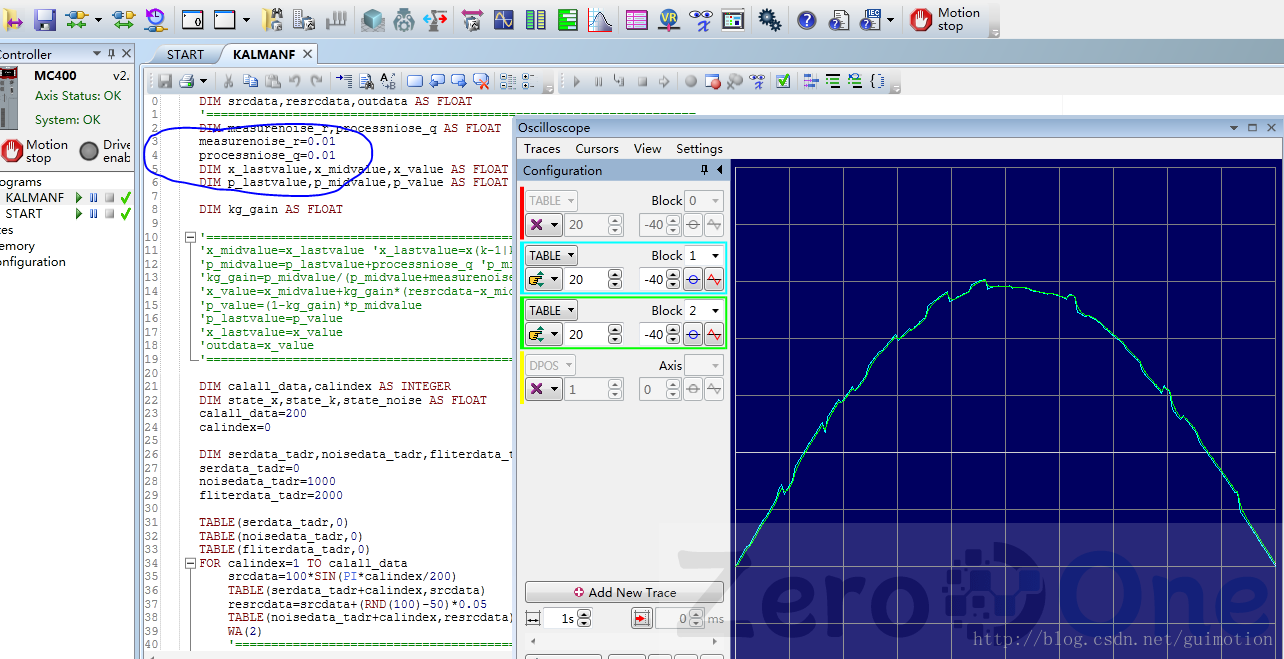
结论:输入和输出基本一致,未有明显的滤波
2、R大 Q小的效果
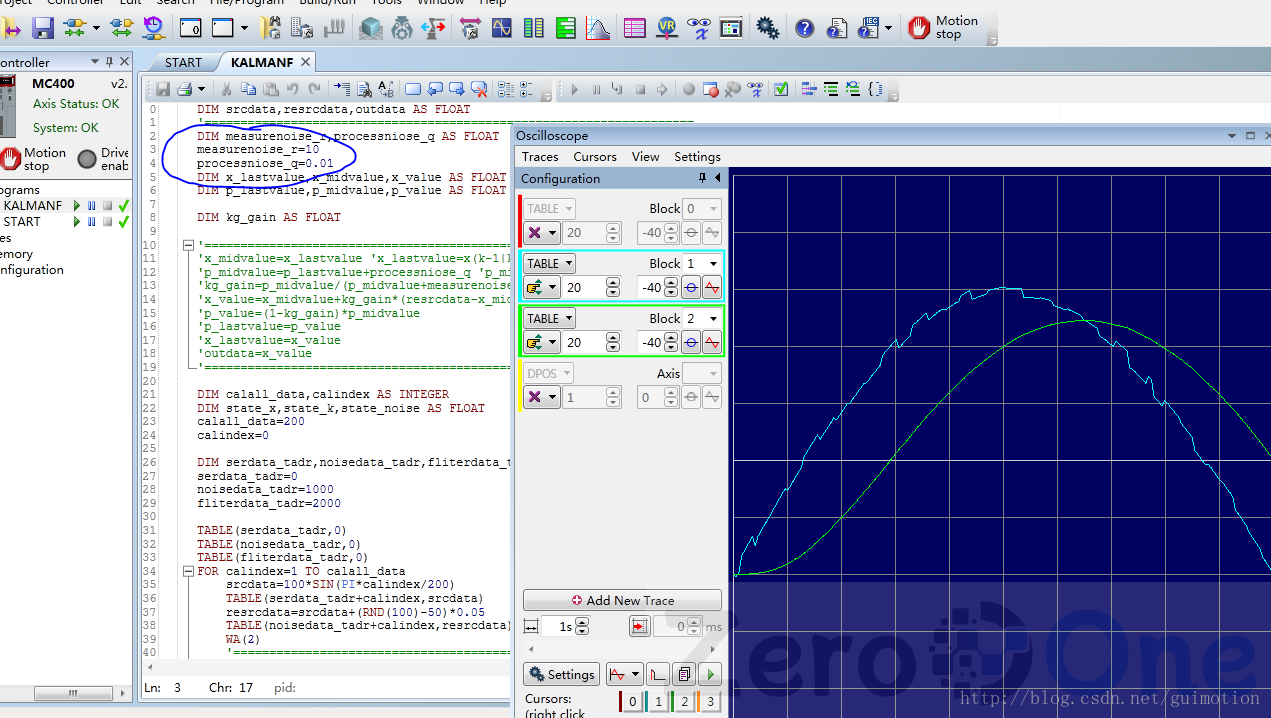
结论:滤波效果明显,但响应滞后比较严重
3、R大 Q大的效果

结论:滤波效果很好,反应了曲线趋势,并又保存了响应性。
卡尔曼属于预测算法,占用运算小,程序执行速度快,非常适合应用与连续滤波算法中。
今天的课程到此结束,谢谢大家的关注,谢谢大家!





