【TRIO-Basic从入门到精通教程二十】Trio通过空间圆弧三点计算圆弧中心和半径
作者:Gmotion
发布时间:2019-03-07
更新时间:2023-12-31
点击数:
兄弟们,大家好。今天给大家带来空间圆弧三点计算圆弧中心和半径公式。
在Trio中,集成了计算函数,今天我们的目的自己来实现这个计算公式。
TRIO圆弧算法实现,对比内置的函数实现。
'导入计算数据 TABLE(100,0,0,0,5,5,5,5,0,0) '自己写算法实现 calcriclecen(100,FALSE) PRINT "XYZ 1=",TABLE(100+10),TABLE(100+11),TABLE(100+12) 'Trio原装算法实现 SPHERE_CENTRE(100+3, 100+6, 100+10) PRINT "XYZ 2=",TABLE(100+10),TABLE(100+11),TABLE(100+12)
Trio指令帮助
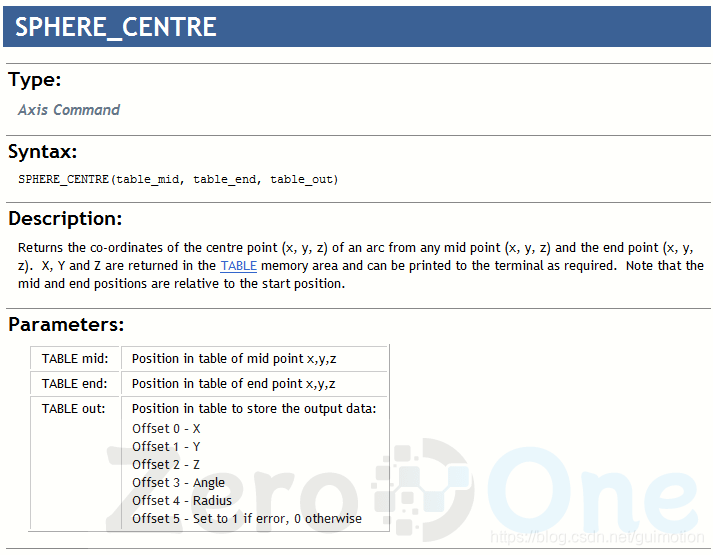
从这个指令能够看出,它的起点必须是0,0,0,这意味着计算必须是增量计算方式。
我们看下我们自己手写的算法:
'=================================================================
'=================================================================
'给定空间三点计算圆弧中心和半径
'partable给定输入参数
'Table0-2 给定P点坐标(起点)
'Table3-5 给定Q点坐标(中点)
'Table6-8 给定Q点坐标(终点)
'Table10-13 输出圆弧中心XYZR
'needprint 确认是否需要打印计算过程数据 false不打印,true打印
FUNCTION calcriclecen(partable AS INTEGER,needprint AS BOOLEAN) AS BOOLEAN
'输入参数检查
IF partable511980 THEN
PRINT "Parameter out of range,Par=",partable
RETURN FALSE
ENDIF
'给定空间三点计算圆弧中心和半径
DIM dpx,dpy,dpz AS FLOAT
dpx=TABLE(partable+0)
dpy=TABLE(partable+1)
dpz=TABLE(partable+2)
DIM dqx,dqy,dqz AS FLOAT
dqx=TABLE(partable+3)
dqy=TABLE(partable+4)
dqz=TABLE(partable+5)
DIM drx,dry,drz AS FLOAT
drx=TABLE(partable+6)
dry=TABLE(partable+7)
drz=TABLE(partable+8)
'打印过程数据
IF needprint THEN
PRINT "========================="
PRINT "Input Parmater:"
PRINT "P [XYZ]=",dpx,dpy,dpz
PRINT "Q [XYZ]=",dqx,dqy,dqz
PRINT "R [XYZ]=",drx,dry,drz
ENDIF
'输出空间原点和半径
DIM dx0,dy0,dz0,dr AS FLOAT
DIM dx1,dy1,dz1 AS FLOAT
dx0=0
dy0=0
dz0=0
dr=0
'-------------------------------------------
DIM pi0,pj0,pk0 AS FLOAT
DIM x1,x2,y1,y2,z1,z2 AS FLOAT
x1=dqx-dpx
x2=drx-dpx
y1=dqy-dpy
y2=dry-dpy
z1=dqz-dpz
z2=drz-dpz
pi0=y1*z2-z1*y2
pj0=z1*x2-x1*z2
pk0=x1*y2-y1*x2
'打印过程数据
IF needprint THEN
PRINT "Proc Parmater:"
PRINT "IJK =",pi0,pj0,pk0
ENDIF
IF (pi0=0) AND (pj0=0) AND (pk0=0) THEN
STOP
ENDIF
'-------------------------------------------
'求PQ和PR的中垂线
'---------------------
'1,过PQ的中点(Mx,My,Mz)
DIM dmx,dmy,dmz AS FLOAT
dmx=(dpx+dqx)/2
dmy=(dpy+dqy)/2
dmz=(dpz+dqz)/2
'与(Mi,Mj,Mk)=(pi,pj,pk)×(x1,y1,z1)垂直
DIM dmi,dmj,dmk AS FLOAT
dmi=pj0*z1-pk0*y1
dmj=pk0*x1-pi0*z1
dmk=pi0*y1-pj0*x1
IF needprint THEN
PRINT "PQ M=",dmi,dmj,dmk
ENDIF
'---------------------
'2,过PR的中点(Nx,Ny,Nz)
DIM dnx,dny,dnz AS FLOAT
dnx=(dpx+drx)/2
dny=(dpy+dry)/2
dnz=(dpz+drz)/2
'与(Ni,Nj,Nk)=(pi,pj,pk)×(x2,y2,z2)垂直
DIM dni,dnj,dnk AS FLOAT
dni=pj0*z2-pk0*y2
dnj=pk0*x2-pi0*z2
dnk=pi0*y2-pj0*x2
IF needprint THEN
PRINT "PR M=",dni,dnj,dnk
ENDIF
'合并计算
DIM ds AS FLOAT
'ds=dNi*dNi+dNj*dNj+dNk*dNk
ds=SQR(pi0*pi0+pj0*pj0+pk0*pk0)
IF ds=0 THEN
dx1=0
dy1=0
dz1=0
ELSE
dx1=pi0/ds
dy1=pj0/ds
dz1=pk0/ds
ENDIF
IF needprint THEN
PRINT "DX1 =",dx1,dy1,dz1,ds
ENDIF
'-------------------------------------------
'得到的两条中垂线为{X=dMx+dMi*tm;Y=dMy+dMj*tm;Z=dMz+dMk*tm;}
'或(x-dmx)/dmi=(y-dmy)/dmj=(z-dmz)/dmk
' {X=dNx+dNi*tn;Y=dNy+dNj*tn;Z=dNz+dNk*tn;}
'或(x-dnx)/dni=(y-dny)/dnj=(z-dnz)/dnk;
'解两直线交点
DIM tm,tn AS FLOAT
tn=((dmy-dny)*dmi+dmj*(dnx-dmx))/(dnj*dmi-dmj*dni)
tm=(dnx+dni*tn-dmx)/dmi
'dx0,dy0,dz0,dr
dx0=INT((dmx+dmi*tm)*100000+0.5)/100000
dy0=INT((dmy+dmj*tm)*100000+0.5)/100000
dz0=INT((dmz+dmk*tm)*100000+0.5)/100000
dr=INT((SQR((dx0-dpx)*(dx0-dpx)+(dy0-dpy)*(dy0-dpy)+(dz0-dpz)*(dz0-dpz)))*100000+0.5)/100000
TABLE(partable+10,dx0,dy0,dz0,dr)
IF needprint THEN
PRINT "Out Parmater:"
PRINT "OUT X Y Z R =",dx0,dy0,dz0,dr
PRINT "========================="
ENDIF
RETURN TRUE
ENDFUNC
'=================================================================通过给定空间三点计算圆弧中心和半径
运行结果测试
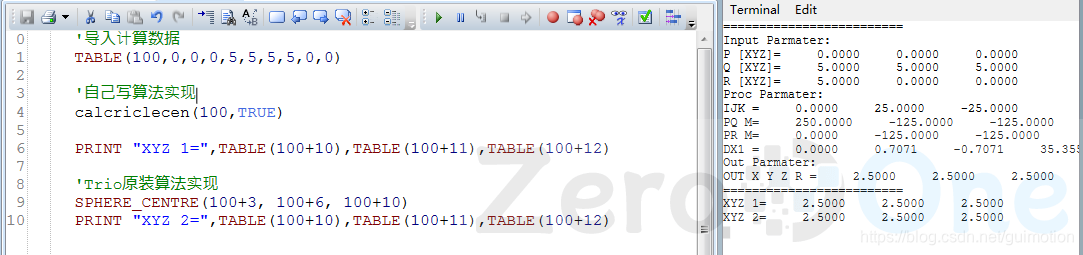
两个方法运行一致!
本次课程任务结束,谢谢大家观看。。。





